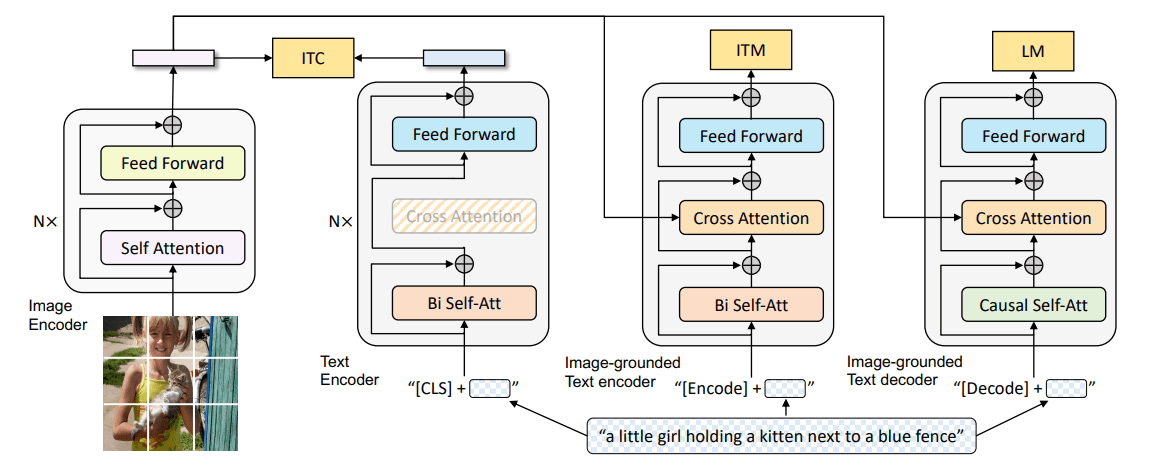
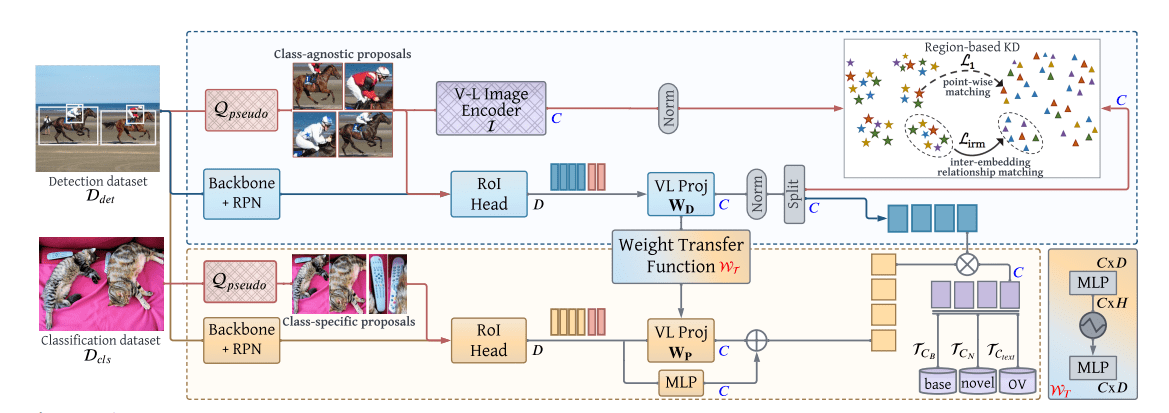
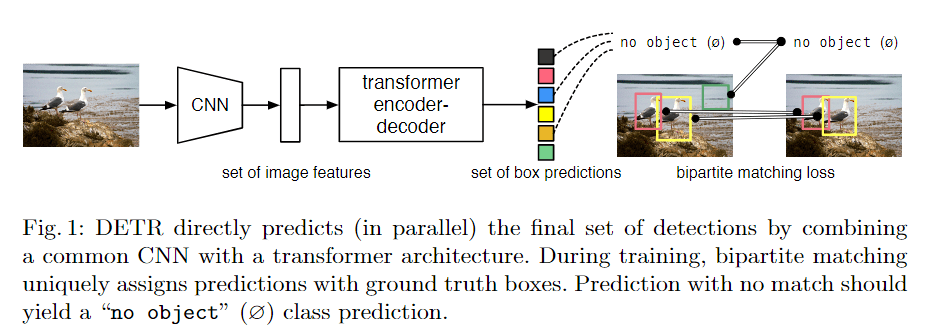
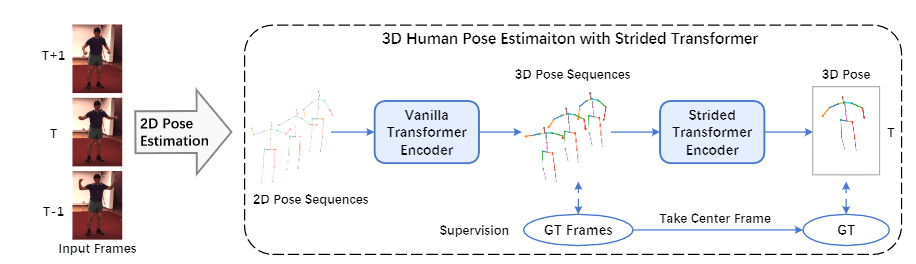
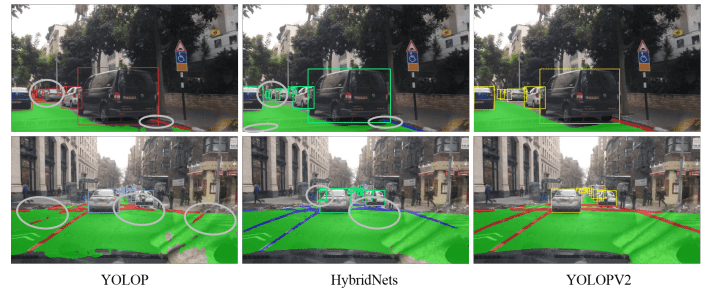
本文提出Earthformer，一个用于地球系统预测的时空Transformer。基于一个时空注意力块，名为立方体注意力。其想法是将数据分解成立方体，并并行应用立方体级的自注意力。

介绍

在本文中，我们提出了Earthformer，一个用于地球系统预测的时空Transformer。为了更好地探索时空注意力的设计，我们提出了立方体注意力，它是高效时空注意力的通用构建模块。其思路是将输入张量分解为不重叠的立方体，并并行应用立方体级的自注意力。

由于我们将 $O(N^2)$ 自注意计算在在局部立方体上，因此整体复杂性大大降低。不同类型的相关关系可以通过不同的立方体分割方案来捕获。通过堆叠具有不同超参数的多个立方体注意力层，我们能够将以前提出的几个视频Transformer归纳为特殊情况，同时也提出了以前没有研究过的新注意力模式。

这种设计的一个局限性是缺乏一个本地立方体相互交流的机制。因此，我们引入了一个全局向量的集合，关注所有的局部立方体，从而收集系统的整体状态。通过关注全局向量，本地立方体可以掌握系统的总体动态，并相互分享信息。

模型

我们将地球系统的预测拟定为一个时空序列预测问题。地球观测数据，如 NEXRAD 的雷达回波图和 CIMP6 的气候数据，被表示为一个时空序列 $[\mathcal{X}_i]^T_{i=1},\mathcal{X}_i \in \mathbb{R}^{H \times W \times C_\text{in}}$ 基于这些观察，模型预测 K步之后的未来 $[\mathcal{Y}_{T+i}]^K_{i=1},\mathcal{Y}_{T+i} \in \mathbb{R}^{H \times W \times C}$ 。

如下图所示，我们提出的Earthformer是一个基于立方体注意力的分层Transformer编码器-解码器。

立方体 Transformer

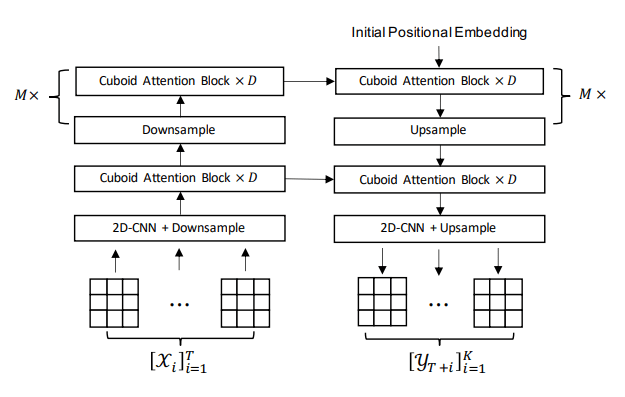
与图像和文本相比，地球系统中的时空数据通常具有更高的维度，例如 3D 的张量 $(T,H,W)$ ，其自注意力计算复杂度则为 $O(T^2H^2W^2)$ ，极其拉跨。

以前的文献[1912.12180,2106.13230,2102.05095]提出了各种结构感知的时空注意力机制，以降低复杂性。这些时空注意机制有一个共同的设计，即堆叠多个基本注意层，这些注意层关注不同类型的数据相关性（例如，时间相关性和空间相关性）。源于这一观察，我们提出了通用的立方体注意层，包括三个步骤。分解、关注 和 合并。

分解

首先对输入张量进行分解 $\mathcal{X} \in \mathbb{R}^{T \times H \times W \times C}$ 到一个立方体序列 ${x^{(n)}}$

{x^{(n)}} = \text{Decompose}(\mathcal{X}, \text{cuboid\_size},\text{strategy},\text{shift})

其中 $\text{cuboid\_size} = (b_T,b_H,b_W)$ 是是局部立方体的大小， $\text{strategy} \in {\text{"local"},\text{"dilated"}}$ 控制是否采用局部分解策略或扩张分解策略， $\text{shift} = (s_T,s_H,s_W)$ 是窗口移位偏移量。下图展示了三个例子，显示了一个输入张量将如何按照 $\text{Decompose}(\cdot)$ 的不同超参数进行分解。

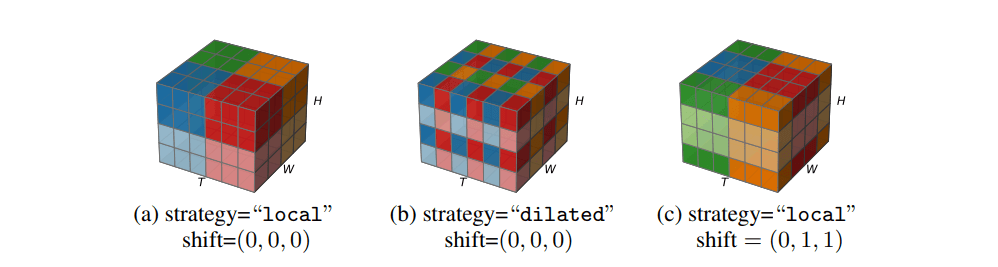
在 $\{\mathcal{X}^{(n)}\}$ 中总共有 $\lceil \frac{T}{b_T}\rceil \lceil\frac{H}{b_H}\rceil\lceil\frac{W}{b_W}\rceil$ 个立方体。为了简化符号我们假设都能被整除，在实践中否则会进行填充。

假设 $x^{(n)}$ 是 $\{x^{(n)}\}$ 中的第 $(n_T,n_H,n_W)$ 个立方体。如果策略是 $\text{local}$ ， $x ^{(n)}$ 的第 $(i, j, k)$ 个元素这样映射到 $\mathcal{X}$ 的 $(i^\prime,j^\prime,k^\prime)$ 个元素

i^\prime \leftrightarrow s_T + b_T(n_T - 1) + i \mod T

j^\prime \leftrightarrow s_H + b_H(n_H - 1) + i \mod H

k^\prime \leftrightarrow s_W + b_W(n_W - 1) + i \mod W

如果策略是 $\text{dilated}$ ，则

i^\prime \leftrightarrow s_T + b_T(i - 1) + n_T \mod T

j^\prime \leftrightarrow s_H + b_H(j - 1) + n_H \mod H

k^\prime \leftrightarrow s_W + b_W(k - 1) + n_W \mod W

由于映射是双向的，我们可以通过逆运算将 $\mathcal{X}$ 中的元素映射到 $\{x^{(n)}\}$ 。

注意力

参加步骤的计算复杂度是 $O(\lceil \frac{T}{b_T}\rceil \lceil\frac{H}{b_H}\rceil\lceil\frac{W}{b_W}\rceil(b_T b_H b_W)^2) \thickapprox O(THW \cdot b_T b_H b_W)$ ，它与立方体大小呈线性扩大。由于立方体的大小可以比输入张量的大小小得多，所以该层比全注意力更有效率。

合并

经过注意力步骤后得到的立方体序列 $\{x^{(n)}\}$ 被合并回原始输入形状，是合并操作中俩公式的逆向操作

\mathcal{X}_out = \text{Merge}(\{x^{(n)}\},\text{cuboid\_size},\text{strategy},\text{shift})

全局向量

前面表述的一个局限性是立方体之间不进行交互。因此，受BERT中采用的 [CLS] 标记的启发，我们建议引入 $P$ 个全局向量 $\mathcal{G} \in \mathbb{R}^{P \times C}$ 的集合，以帮助立方体分散并收集关键的全局信息。当每个立方体进行自我关注时，这些元素不仅会关注同一立方体中的其他元素，还会关注全局向量 $\mathcal{G}$ 。我们将修改自注意力，以实现局部-全局信息交换。