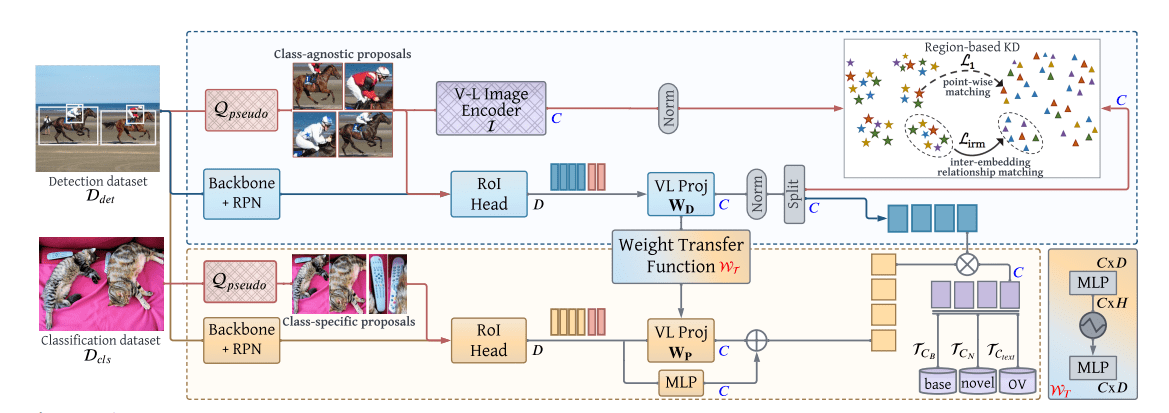
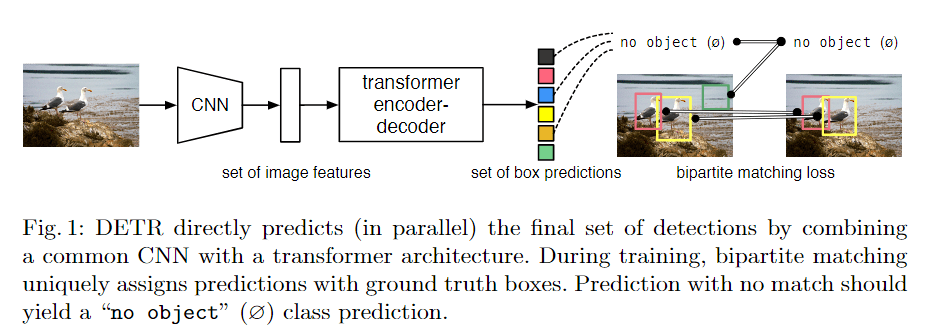
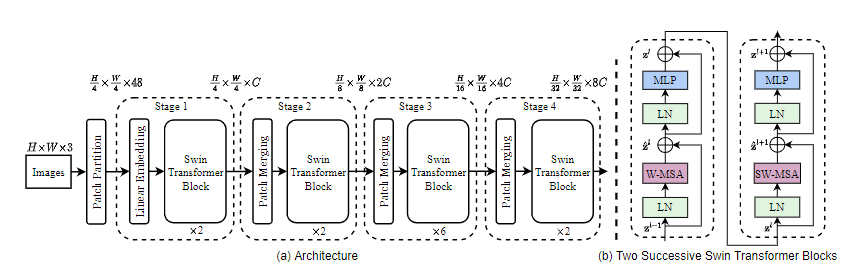
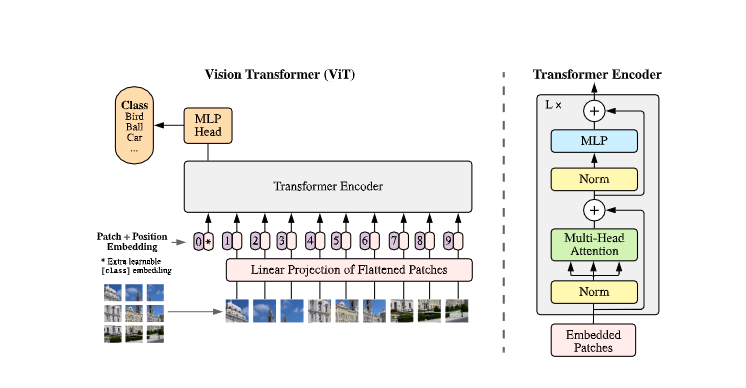
介绍

我们提出了一个新的基于Transformer的3D人体姿势估计架构，称为Strided Transformer，它可以简单有效地将一个长的2D姿势序列提升到一个单一的3D姿势。

为了减少序列冗余和计算成本，引入了Strided Transformer Encoder(STE)来逐步减少时间维度，并将长距离信息以分层的全局和局部方式聚合到姿势序列的单向量表示中。

设计了一个full-to-single的监督方案，在全序列规模的训练中施加额外的时间平滑性约束，并进一步完善单一目标帧规模的估计。

方法

给定从视频中估计出的2D位置序列 $P=\{p_1,...p_T\}$ 我们旨在重建目标帧的三维关节位置 $X \in \mathbb{R}^{J \times 3}$ ，其中 $p_t \in \mathbb{R}^{J \times 2}$ 表示 $t$ 帧处的2D关节位置， $T$ 是视频帧的数量， $J$ 是关节的数量。

该网络包含一个普通Transformer编码器（VTE），然后是一个跨步Transformer编码器（STE），VTE首先被用来对长距离信息进行建模，并由全序列尺度进行监督，以强制实现时间上的平滑性，然后，本文提出的STE聚合信息以产生一个目标姿势表示，并由单个目标帧的尺度监督以产生更准确的估计。

跨步 `Transformer` 编码器

本文提出了一种逐步压缩隐藏状态的序列，在分层结构中对全局和局部信息进行建模的STE。其每一层都由一个多头自我注意（MSA）和一个卷积前馈网络（CFFN）组成。

卷积前馈神经网络

给定 $T$ 个序列与 $D_in$ 个通道的输入特征向量 $Z \in \mathbb{R}^{T \times D_{in}}$ ，去生成一个 $(\tilde{T}, D_{out})$ 的特征，FFN中FC所进行的操作可以被表述为：

\text{FC}_{t,d_{out}} = \sum^{D_{in}}_{i} w_{d_{out},i} * z_{t, i}

如果考虑到1D卷积，核大小为 $K$ ，跨步因子为 $S$ ，那么CFFN中的分层卷积可以计算为：

\text{Conv}_{S(t),c_{out}(Z)} = \sum^{D_{in}}_i \sum^K_k w_{d_{out},i,k} * z_{S(t-\frac{K-1}{2}+k),i}

这样一来，VTE的FFN中的全连接层就被分层卷积取代了。修改后的VTE被命名为Strided Transformer Encoder（STE），可以表示为：

\hat{Z}^{n-1} = Z^{n-1} + \text{MSA}(\text{LN}(Z^{n-1}))

\hat{Z}^n = Z^n + \text{MaxPool}(\hat{Z}^{n-1}) + \text{CFFN}(\text{LN}(\hat{Z}^{n-1}))

其中 $n \in [1,...,N]$ 是STE的层序号

网络架构

Pose embedding

姿势嵌入首先将每一帧的 $J$ 点的 $(x,y)$ 坐标连接到标记 $P^\prime \in \mathbb{R}^{T \times (J \cdot 2)}$ ，然后使用具有dm通道的1D卷积层将每个token嵌入到高维特征 $Z-0 \in \mathbb{R} ^{T \times d_m}$ ，然后进行批量归一化、dropout和ReLU激活。

VTE

假设VTE由N1层组成，在VTE的第一层之前使用可学习的位置嵌入 $E_1 \in \mathbb{R}^{T \times d_m}$ ，可以表述如下：

Z^0_1 = Z_0 + E_1

然后，给定嵌入特征z^0_1，VTE层可以表示为：

\hat{Z}^{n-1}_1 = Z^{n-1}_1 + \text{MSA}(\text{LN}(Z^{n-1}_1))

Z^n_1 = \hat{Z}^{n-1}_1 + \text{FFN}(\text{LN}(\hat{Z}^{n-1}_1))

它可以通过使用一个函数 $\text{VTE}(\cdot)$ 来表示VTE层：

Z^n_1 = \text{VTE}()Z^{n-1}_1

STE

它是建立在VTE输出的基础上，使用 $Z^{N_1}_1 \in \mathbb{R}^{T \times d_m}$ 作为输入，由于序列长度的不同，STE的每一层都使用了可学习的位置嵌入 $E_2 \in \mathbb{R}^{S(t) \times d_m}$ ，其分层因子为 $S$ 。那么，STE层可以表示为：

Z^n_2 = \text{STE}(Z^{n-1}_2 + E^n_2)

回归头

最后，3D姿势预测的输出是 $\tilde{X}$ 和 $X$ ，其中 $\tilde{X} \in \mathbb{R}^{T \times J \times 3}$ 和 $X \in \mathbb{R}^{J \times 3}$ 分别是3D姿势序列的预测和目标帧的3D关节定位。

`FUll-to-Single` 预测

全序列尺度（Full sequence scale）

序列损失 $\mathcal{L}_f$ 被用来改进单帧预测，以实现序列的时间一致性。这个损失保证了估计的三维位置序列 $\hat{X} \in \mathbb{R}^{T \times J \times 3}$ 与ground truth三维连接序列 $T \in \mathbb{R}^{T \times J \times 3}$ 相吻合：