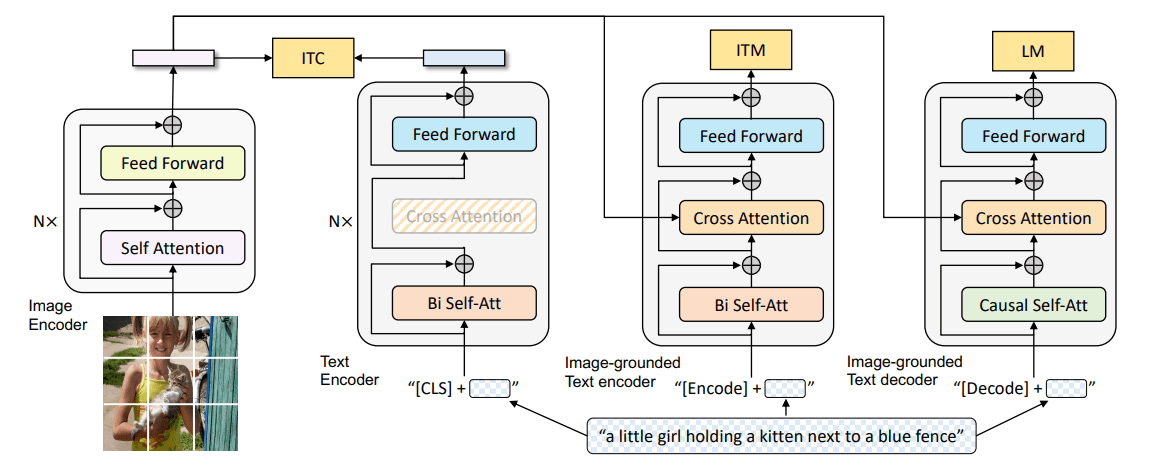
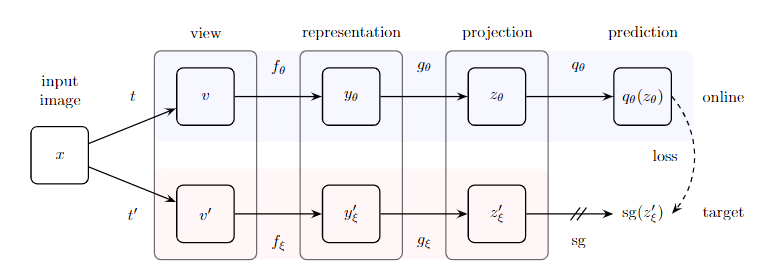
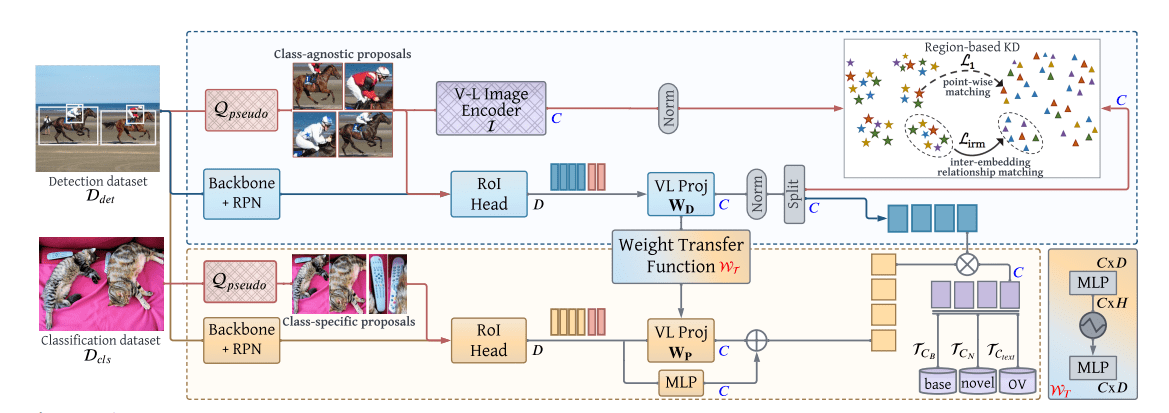
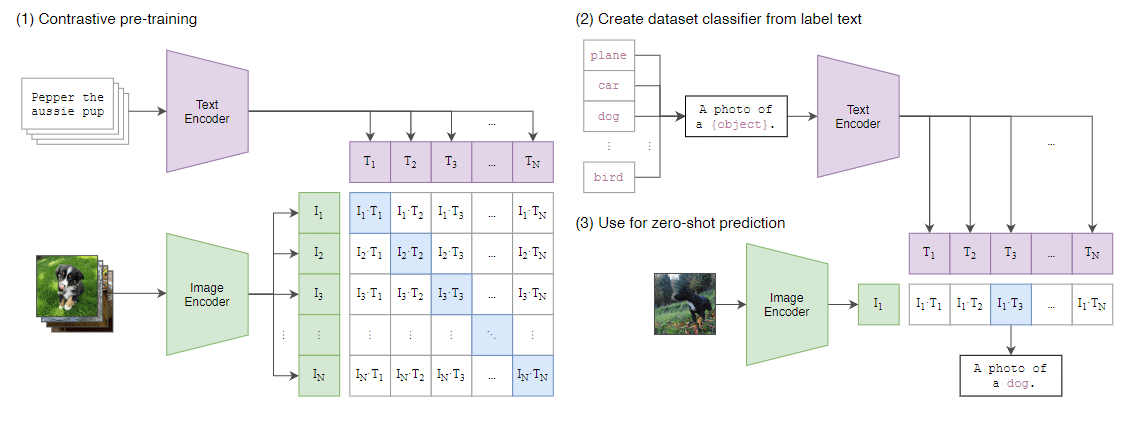
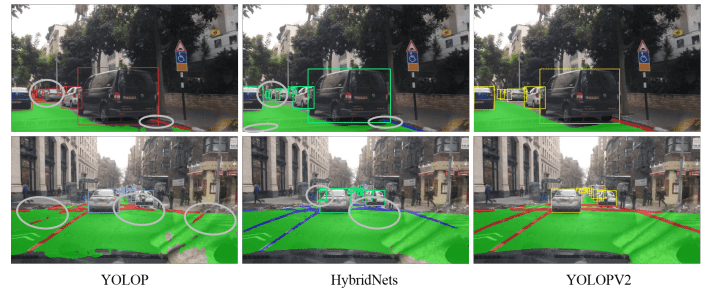
完全形法的主要思想是，从一个初始基本可行解开始，迭代改进可行解，直到达到最优。

基本概念

对于线性规划的标准形式：

min⁡f≡cxs.t.Ax=bx≥0\begin{aligned} \min &&f &\equiv cx \\ \text{s.t.}&& Ax&=b \\ && x &\geq 0 \end{aligned}

通过变换行，使其前 mm 行线性无关，对矩阵AA的分割，得到基矩阵 BB 与非基矩阵 NN：

Am×n=(P1,P2,...,Pm,Pm+1,...,Pn)=(B,N)\underset{m \times n}{A} = (P_1,P_2,...,P_m,P_{m+1},...,P_n) = (B,N)

同样对CC、xx进行划分得到(CB,CN)(C_B,C_N) (xB,xN)(x_B,x_N)

初始基本可行解

取一个基本可行解

x(0)=(B−1b0),B−1b≥0x^{(0)} = \left( \begin{array}{c} B^{-1}b \\ 0 \end{array} \right) ,B^{-1}b \geq 0

其目标函数值为

f0=cx(0)=(CB,CN)(B−1b0)=CBB−1b(1)f_0 =cx^{(0)} = (C_B, C_N) \left( \begin{array}{c} B^{-1}b \\ 0 \end{array} \right) = C_BB^{-1}b \tag{1}

进基变量、出基变量

通过将基向量中的值与非基向量中的值位置进行替换，以改进基本可行解

(PB1,...,PBr,...,PBm,PN1,...,PNk,...,PNn−m)(P_{B_1},...,P_{B_r},...,P_{B_m},P_{N_1},...,{P_{N_k},...,P_{N_{n-m}}})

将基向量 PBrP_{B_r} 与非基向量 PNkP_{N_k} 位置进行变换，则称 PBrP_{B_r} 为出基向量，PNkP_{N_k} 为进基向量。对于同样位置的 xBrx_{B_r} 称为出基变量，xNkx_{N_k} 称为进基变量。

单纯形法

单纯形法从一个初始可行解开始，通过选取出基向量与进基向量以迭代改进可行解，不停迭代直到达到最优解，所以需要解决三个问题：

  • 确定进基的下标 NkN_k
  • 确定出基的下标 BrB_r
  • 确定进基变量的值，（出基变量被人为设定为00）

确定进基变量/向量的下标

根据等式约束，可得：

Ax=b(B,N)(xBxN)=bBxB+NxN=bxB=B−1b−B−1NxN(2)\begin{aligned} Ax &=b \\ (B,N) \left( \begin{array}{c} x_B \\ x_N \end{array} \right) &=b \\ Bx_B + Nx_N&=b \\ x_B &= B^{-1}b-B^{-1}Nx_N \tag{2} \end{aligned}

目标函数值为：

f=cx=CBxB+CNxN=CB(B−1b−B−1NxN)将式 (2) 代入=CBB−1b−(CBB−1N−CN)xN=f0−∑j∈R(CBB−1Pj−Cj)xj,R={N1,N2,...,Nn−m}将矩阵相减与向量内积写为对应分量相减相乘累加=f0−∑j∈R(zj−cj)xj因为 CBB−1Pj 都已知，是常量，以 zj 代换\begin{aligned} f=cx&=C_Bx_B + C_Nx_N \\ &= C_B(B^{-1}b-B^{-1}Nx_N) &&\text{将式 (2) 代入} \\ &= C_BB^{-1}b - (C_BB^{-1}N-C_N)x_N \\ &= f_0 - \sum_{j \in R}(C_BB^{-1}P_j-C_j)x_j,R=\{N_1,N_2,...,N_{n-m}\} &&\text{将矩阵相减与向量内积写为对应分量相减相乘累加} \\ &= f_0 - \sum_{j \in R}(z_j-c_j)x_j &&\text{因为 $C_BB^{-1}P_j$ 都已知，是常量，以 $z_j$ 代换} \end{aligned}

目标函数的值只与 xNx_N 有关（xBx_B 的影响隐含在 xNx_N 的变化中），为了改进目标函数的值，需要使 ∑j∈R(zj−cj)xj\sum_{j \in R}(z_j-c_j)x_j 在满足约束的情况下最大。

此时考虑两种情况：

  1. ∀j,zj−cj≤0\forall j,z_j-c_j \leq 0 因为 xj≥0x_j \geq 0 所以此时已经最大，即目标函数值已经最小，达到最优，停止迭代。
  2. ∃j,zj−cj>0\exists j, z_j - c_j > 0 取 zk−ck=max⁡j∈R{zj−cj}z_k - c_k = \underset{j \in R}{\max}\{z_j-c_j\}，PNkP_{N_k} 与xkx_k进基。
    只改变了xkx_k的值，而其他变量仍然人工设置为0，
    此时目标函数值为：

f=f0−(zk−ck)xk(3)f = f_0 - (z_k-c_k)x_k \tag{3}

此时 xBx_B 的值变为：

xB=B−1b−B−1PNkxkx_B = B^{-1}b - B^{-1}P_{N_k}x_k

令 bˉ=B−1b\bar{b} = B^{-1}b，yk=B−1PNk={y1k,...,ym−nk}y_k = B^{-1}P_{N_k} = \{y_{1k},...,y_{m-nk}\}，上式又可以写为：

xB=bˉ−ykxk(4)x_B = \bar{b} - y_kx_k \tag{4}

确定进基变量的值与出基向量/变量的下标

为了使目标函数（式(3)(3)）最小，因为 zl−ckz_l-c_k 的值确定，所以需要让 xkx_k 在满足约束的情况下最大，即，保证 xB=bˉ−ykxk≥0x_B=\bar{b} - y_kx_k \geq 0，其中 bˉ≥0\bar{b} \geq 0。
根据式(4)(4)，此时考虑两种情况:

  1. ∀i,yik≤0\forall i,y_{ik} \leq 0 无论 xkx_k 取什么值，都能保证 xB≥0x_B \geq 0，即 xkx_k 可以取任意值
  2. ∃i,yik>0\exists i,y_{ik} > 0 需要使 bˉi−yikxk≥0\bar{b}_i-y_{ik}x_k \geq 0 即 xk≤bˉiyikx_k \leq \frac{\bar{b}_i}{y_{ik}} 为了使 xkx_k 最大且满足约束，取 xk=min⁡{bˉiyik∣y>0}x_k = \min\{\frac{\bar{b}_i}{y_{ik}} | y > 0\} 若设最小的 bˉiyik\frac{\bar{b}_i}{y_{ik}} 下标为 rr，xk=bˉryrkx_k = \frac{\bar{b}_r}{y_{rk}}，同时 rr 也是出基向量/变量的下标。

此时新的基本可行解（保证可行可通过证明基矩阵仍然线性无关，证明略）为：

x=(xB1,...,xBr−1,0,xBr+1,...,xBm,0,...,0,xk,...,0)x=(x_{B_1},...,x_{B_{r-1}},0,x_{B_{r+1}},...,x_{B_m},0,...,0,x_k,...,0)

https://www.bilibili.com/video/BV1e64y1Y7Sr