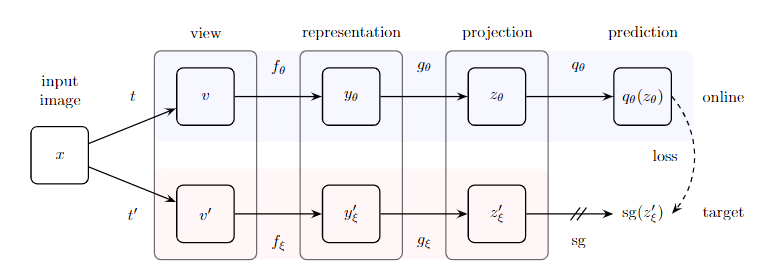
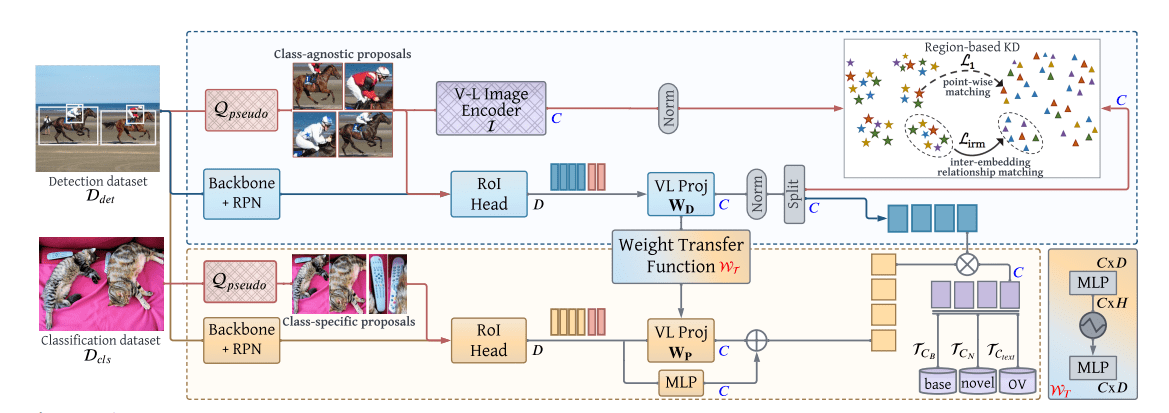
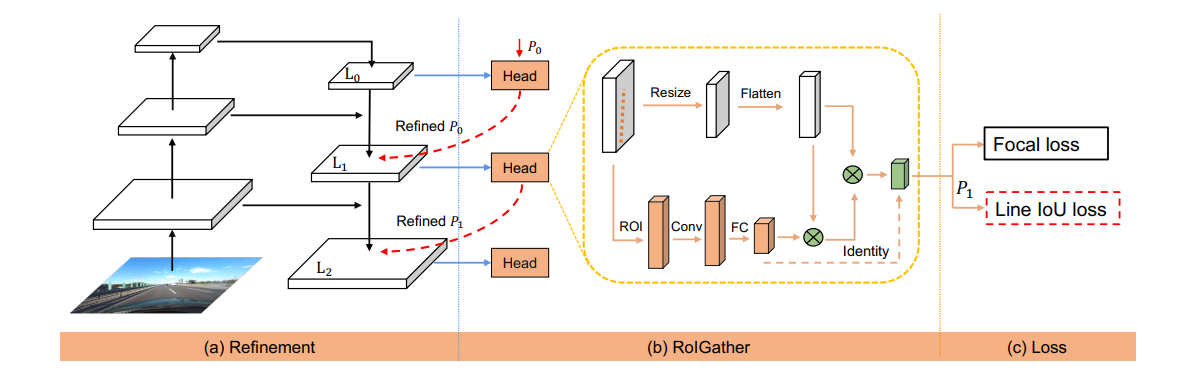
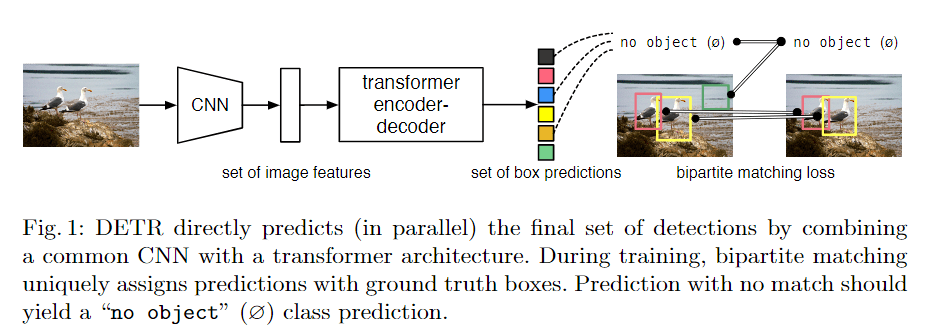
本文提出了新的视屏对象分割架构 XMem，使用同一的特征记忆存储，包含多个独立但深度连接的记忆存储：

  • 快速更新（每帧）的感官记忆。
  • 高分辨率的工作记忆。
  • 紧凑的持续长期记忆。

同时开发了一个记忆增强算法。

介绍

先前的SOTA精度高，但内存占用也高，不适合长视频。用于长视频的架构抛弃了一部分精度，效果不佳——这种性能与内存消耗的不良联系时因为单一的功能的记忆。

我们提出一种统一的记忆架构，受 Atkinson–Shiffrin 记忆模型[Human Memory: A Proposed System and its Control Processes]的启发，该模型假设人类记忆由三个部分组成，XMem维护着三个独立但紧密连接的特征记忆存储：

  • 快速更新的感官记忆：每帧更新一次。
  • 高分辨率的工作记忆：存储大小固定，如果已满，则整合到长期记忆。
  • 紧凑的持续长期记忆：在数千帧后，长期记忆也满时，丢弃过时的特征，以限制GPU内存使用量。

方法

概览

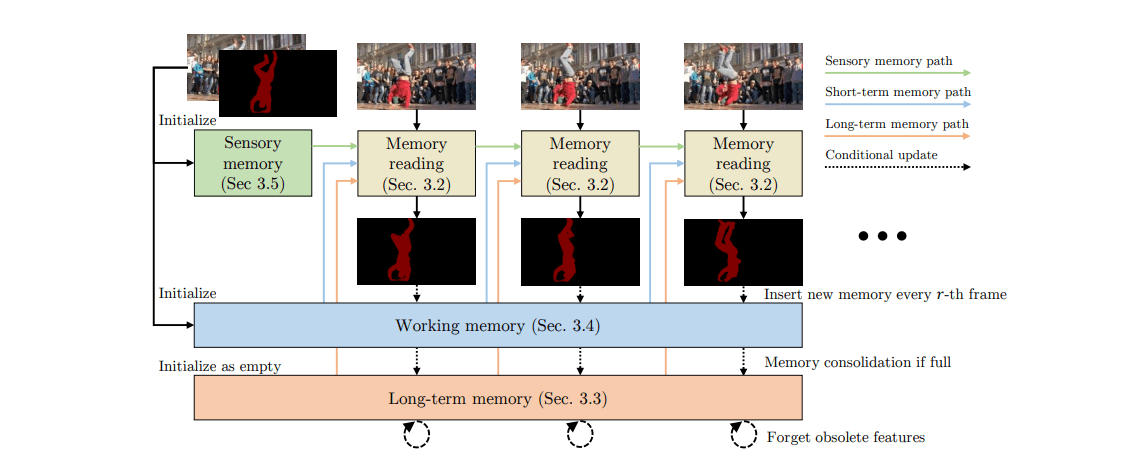
为了提高可读性，我们考虑单个目标对象。给定第一帧（图 2 左上角）的图像和目标对象掩码，XMem跟踪对象并为后续查询帧生成其掩码。

在第一帧，使用输入初始化不同的特征记忆存储。

对于每个后续查询帧，我们分别从三个记忆存储执行记忆读取。从所有三个记忆存储中提取相关特征，并使用这些特征生成掩码。

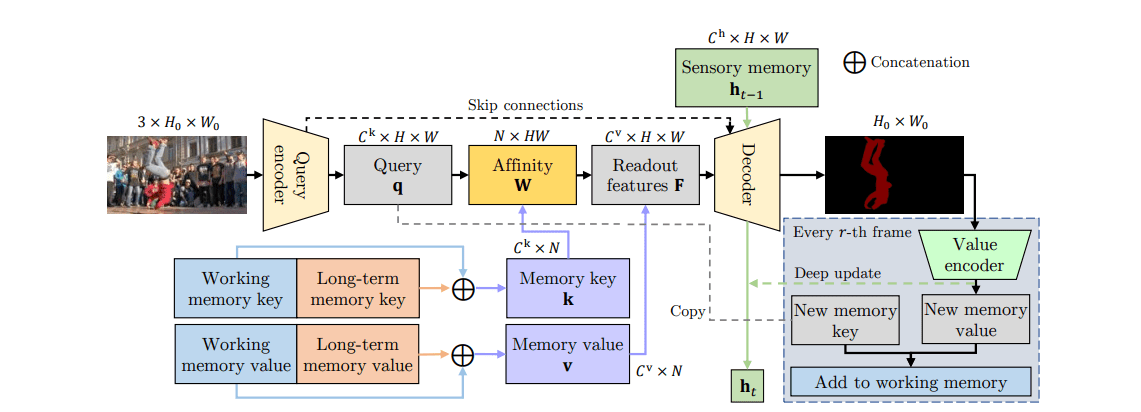
XMem 由三个端到端的可训练CNN组成：

  • 查询编码器：提取特定用于查询的图像（查询帧的输入）特征。
  • 解码器：采用记忆读取步骤的输出来生成对象掩码。
  • 值编码器：将图像与对象掩码相结合以提取新的记忆特征。

内存读取

记忆中的键和值集合简单地实现为最后一个维度中的拼接：k=kw⊕klt\text{k} = \text{k}^\text{w} \oplus k^\text{lt} 和 v=vw⊕vlt\text{v} = \text{v}^\text{w} \oplus \text{v}^\text{lt}，其中上标 w\text{w} 和 lt\text{lt} 分别表示工作记忆和长期记忆。

工作记忆由键 kw∈RCk×THW\text{k}^\text{w} \in \mathbb{R}^{C^\text{k} \times THW} 和值 vw∈RCv×THW\text{v}^\text{w} \in \mathbb{R}^{C^\text{v} \times THW} 组成，其中TT是工作记忆帧的数量。

长期记忆同样由键 klt∈RCk×L\text{k}^\text{lt} \in \mathbb{R}^{C^\text{k} \times L} 和值 klt∈RCv×L\text{k}^\text{lt} \in \mathbb{R}^{C^\text{v} \times L} 组成。其中 LL 是长期记忆``原型的数量。

工作记忆和长期记忆中的元素总数为 N=THW+LN = THW + L。

掩码通过将上一帧的短期感官记忆 ht−1∈RCh×H×W\text{h}_{t-1} \in \mathbb{R}^{C^h \times H \times W} 和存储在长期记忆与工作记忆中的信息 F∈RCv×H×W\text{F} \in \mathbb{R}^{C^v \times H \times W}（通过读出操作计算） 作为输入的解码器计算。

读出操作：

F=vW(k,q)\text{F} = \text{v}\text{W}(\text{k},\text{q})

其中 k∈RCk×N\text{k} \in \mathbb{R}^{C^\text{k} \times N}，v∈RCv×N\text{v} \in \mathbb{R}^{C^v \times N} 为 NN 个存储在长期记忆和工作记忆中的 CkC^\text{k}-维的键 和 CvC^v-维的值。W(k,q)\text{W}(\text{k},\text{q}) 是形状为 N×HWN \times HW 的亲和矩阵（由相似性矩阵进行softmax得出），表示由键 k\text{k} 控制的读出操作，以及通过查询编码器从查询帧获得的查询帧 q∈RCk×HWq \in \mathbb{R}^{C^\text{k} \times HW} 的查询。

亲和矩阵是通过对相似性矩阵 S(k,q)\text{S}(\text{k},\text{q}) 的记忆维度（行）应用softmax来获得的，该矩阵包含每个键元素和每个查询元素之间的成对相似性。

我们提出了新的相似性函数各向异性L2，引入两个缩放项打破键与查询之间的对称性。

具体而言，键与缩放项 s∈[1,∞)Ns \in [1,\infty)^N 相关联，查询与选择项 e∈[0,1]Ck×HWe \in [0,1]^{C^\text{k} \times HW} 相关联。第 ii 个键元素和第 jj 个查询元素之间的相似性计算为：

S(k,q)ij=−si∑cCkecj(kci−qcj)\text{S}(\text{k},\text{q})_{ij} = -\text{s}_i\sum^{C^\text{k}}_c \text{e}_{cj}(\text{k}_{ci} - \text{q}_{cj})

收缩项 s\text{s} 直接缩放相似性并显式编码置信度（高收缩表示低置信度），并导致更局部的影响。

如果查询恰好与低置信度键重合，即使是低置信度键也可能具有很高的贡献，从而避免了点积的内存支配问题。不同地，选择项 e\text{e} 控制关键空间中每个通道的相对重要性，以便将注意力放在更具区分性的通道上。

选择项 e\text{e} 由查询编码器与查询 q\text{q} 一起生成。收缩项 s\text{s} 与工作记忆和长期记忆中的键 k\text{k} 和值 v\text{v} 一起收集。

长期记忆

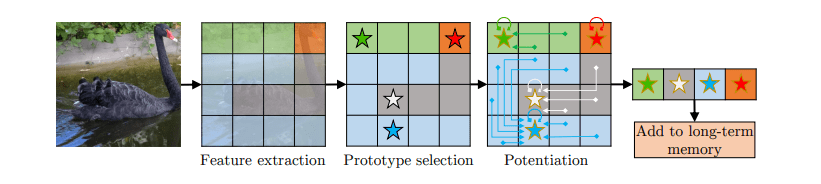
动机

为了存储一组紧凑且具有代表性的记忆特征，我们设计了一个记忆巩固程序，从工作存记忆中选择原型，并用记忆增强算法来丰富它们，当工作记忆达到预定的大小 TmaxT_\text{max} 时，我们进行记忆巩固。第一帧（有用户提供的ground truth）和最近的 Tmin−1T_{min} - 1 个记忆帧将作为高分辨率的缓冲区保留在工作记忆中，而其余的（Tmax−TminT_\text{max} - T_\text{min} 帧）则是被转化为长期记忆表示的候选键 kc⊂kw\text{k}^\text{c} \subset \text{k}^\text{w}，和候选值 vc⊂vw\text{v}^\text{c} \subset \text{v}^\text{w}。

原型选择

我们从候选者中抽出一个有代表性的小子集 kp⊂kc\text{k}^\text{p} \subset \text{k}^\text{c} 作为原型。我们挑选最经常使用的候选人作为原型。 记忆元素的使用情况由其在亲和矩阵中的累积总亲和力（概率质量）来定义，并由每个候选人在工作记忆中的持续时间来归一化。每个候选者的持续时间至少是 r⋅(Tmin−1)r \cdot (T_\text{min} - 1)，导致稳定的使用统计。我们得到这些原型的键为 kp∈RCk×P\text{k}^\text{p} \in \mathbb{R}^{C^\text{k} \times P}。

记忆增强

我们从候选键 kc\text{k}^\text{c} 中抽取的原型键 kp\text{k}^\text{p} 既稀疏又离散。如果我们以同样的方式对原型值 vp\text{v}^\text{p} 进行抽样，所得到的原型值将不可避免地对其他候选人的代表性不足，并容易产生混叠（aliasing）。 防止混叠的常用技术是应用一个抗混叠（如高斯）滤波器。我们在高维（Ck）C^\text{k}） 键空间中构建过滤邻域，这样就可以利用密钥 kp\text{k}^\text{p} 和 kc\text{k}^\text{c} 给出的高表现力邻域信息。

具体来说，对于每个原型，我们通过加权平均从所有的候选值 vc\text{v}^\text{c} 中汇总数值。权重的计算是通过对键相似度的softmax来进行的。同样使用各向异性L2计算。通过用候选键 kc\text{k}^\text{c} 代替记忆键 k\text{k}，用原型键 kp\text{k}^\text{p} 代替查询 q\text{q}，我们得到相似度矩阵 S(kc,kp)S(\text{k}^\text{c},\text{k}^\text{p})。和以前一样，我们使用softmax来获得亲和矩阵W(kc,kp)W(\text{k}^\text{c},\text{k}^\text{p})（其中每个原型对应于候选人的分布)。然后，我们通过以下方法计算出原型值vp\text{v}^\text{p}

vp=vcW(kc,kp)\text{v}^\text{p} = \text{v}^\text{c} \text{W}(\text{k}^\text{c},\text{k}^\text{p})

最后，kp\text{k}^\text{p} 和 vp\text{v}^\text{p} 分别被附加到长期记忆的 klt\text{k}^\text{lt} 和 klt\text{k}^\text{lt} 中。

工作记忆

工作记忆将高分辨率的特征存储在一个临时缓冲区中。它有助于在几秒钟的时间范围内进行准确的匹配。

我们的内存读取``工作内存由键 kw∈RCk×THW\text{k}^\text{w} \in \mathbb{R}^{C^\text{k} \times THW} 和值 vp∈RCv×THW\text{v}^\text{p} \in \mathbb{R}^{C^\text{v}\times THW} 组成，其中 TT 是工作记忆帧的数量。键是由图像编码的，并与查询 q\text{q} 驻留在同一嵌入空间，而值是由图像和掩码编码的。

在每一个第rr帧，我们

  1. 复制查询作为一个新的键
  2. 通过将图像和预测的掩码输入值编码器来产生一个新的值。新的键和值被附加到工作记忆中，并在随后的帧中用于记忆读取。

我们限制工作存储器中的帧数 T:Tmin≤T<TmaxT:T_\text{min} ≤ T < T_\text{max}

感官记忆

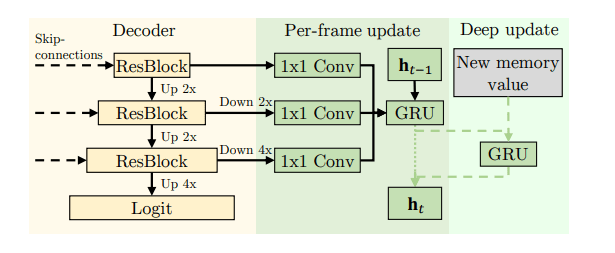
感官记忆侧重于短期，并保留低级信息，如物体位置。

具体而言，感觉记忆存储一个隐藏表示 ht∈RCh×H×W\text{h}_t \in \mathbb{R}^{C^\text{h} \times H \times W}，初始化为零向量，并由GRU传播。 这种感官记忆使用解码器的多尺度特征每帧更新一次。在每个第 rr 帧中，每当生成新的工作记忆帧时，我们都会执行深度更新。来自值编码器的特征用于使用另一个 GRU 刷新感官记忆。这允许感官存储器

  1. 丢弃已经保存到工作记忆中的冗余信息。
  2. 以最小的开销从值编码器接收更新，因为我们正在重用现有特征。

符号表

符号 描述
TT 工作记忆中帧的数量
H0H_0,W0W_0 输入图像的高宽
q∈RCk×HWq \in \mathbb{R}^{C^\text{k} \times HW} 查询编码器输出的特征图
kw∈RCk×THW\text{k}^\text{w} \in \mathbb{R}^{C^\text{k}\times THW},vw∈RCv×THW\text{v}^\text{w} \in \mathbb{R}^{C^\text{v}\times THW} 工作记忆中的键和值，上标 w\text{w} 代表工作记忆
klt∈RCk×L\text{k}^\text{lt} \in \mathbb{R}^{C^\text{k}\times L},vlt∈RCv×L\text{v}^\text{lt} \in \mathbb{R}^{C^\text{v}\times L} 长期记忆中的键和值，上标 lt\text{lt} 代表长期记忆
N=THW+LN = THW + L 工作记忆和长期记忆中的元素的总数
k∈RCk×N\text{k} \in \mathbb{R}^{C^\text{k} \times N},v∈RCv×N\text{v}\in \mathbb{R}^{C^\text{v} \times N} 记忆中键和值的集合，由工作记忆与长期记忆的键和值沿最后一个维度拼接而成
ht∈RCh×H×Wh_t \in \mathbb{R}^{C^\text{h} \times H \times W} tt 帧时的感官记忆
S(k,q)\text{S}(\text{k},\text{q}) 用各向异性L2计算相似信的相似性矩阵
W(k,q)\text{W}(\text{k},\text{q}) 亲和矩阵，由对相似性矩阵的行维度应用softmax得到
TminT_\text{min} 工作记忆记忆整合保留最近的帧的数量
TmaxT_\text{max} 工作记忆最大大小
kc⊂kw\text{k}^\text{c} \subset \text{k}^\text{w} 候选键，总共 Tmax−TminT_\text{max} - T_\text{min} 帧
vc⊂vw\text{v}^\text{c} \subset \text{v}^\text{w} 候选值，总共 Tmax−TminT_\text{max} - T_\text{min} 帧
kp⊂kc\text{k}^\text{p} \subset \text{k}^\text{c},kp∈RCk×P\text{k}^\text{p} \in \mathbb{R}^{C^\text{k} \times P} 原型，候选者中有代表性的小子集

https://arxiv.org/abs/2207.07115v2

https://github.com/hkchengrex/XMem