介绍

现在的ConvNets网络越来越复杂，尽管许多复杂的ConvNets比简单的提供更高的精度，但缺点也很明显：

多分支结构使得该模型难以实施和定制（需要保持特征图大小不变），减缓推理速度，降低内存利用率。
一些组件（例如Xception和MobileNets中的depth-wise卷积和ShuffleNets中的channel shuffle）增加了内存访问成本并缺乏对各种设备的支持。

由于影响推理速度的因素太多，浮点运算量（FLOPs）并不能准确反映实际速度。

本文中，我们提出了RepVGG，一种VGG风格的架构，其性能优于许多复杂的模型（图1）。RepVGG具有以下优点：

该模型有一个类似于VGG的普通拓扑结构，没有任何分支，这意味着每一层都将其唯一的前一层的输出作为输入，并将输出输入其唯一的后一层。
模型主体只使用了 $3 \times 3$ conv和ReLU。
具体的架构（包括具体的深度和层宽）被实例化，没有NAS、手动细化、复合缩放[，也没有其他重度设计。

由于多分支结构的好处都是易于训练，训练时用多分支结构来提升网络性能，而推理时，利用结构重参数化，变换为单路结构。

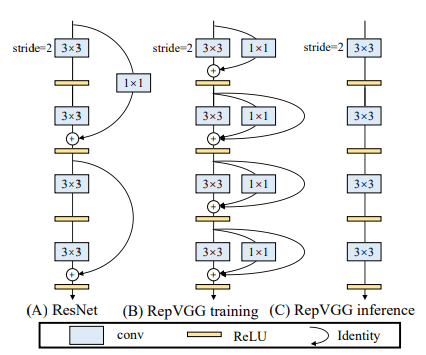
详细来说，训练时RepVGG使用Identity链接和 $1 \times 1$ conv分支，它的灵感来自于ResNet，但方式不同，可以通过结构上的重新参数化来删除分支，如上图。训练结束后，我们用简单的代数变换，Identity分支可以被转换为为退化的 $1 \times 1$ conv $1 \times 1$ conv 可以进一步被视为退化的 $3\times 3$ conv，这样我们就可以用训练时参数构建一个仅有 $3 \times 3$ 卷积的单分支网络，它被保存起来用于测试和部署。

本文的贡献总结如下：

提出了一个一个简单的架构，与最先进的技术相比，具有良好的速度-准确度权衡的RepVGG
我们建议使用结构性重参数化，将训练时的多分支拓扑结构与推理时的普通结构解耦。
我们展示了RepVGG在图像分类和语义分割中的有效性，以及实施的效率和简易性。

通过结构重构构建RepVGG

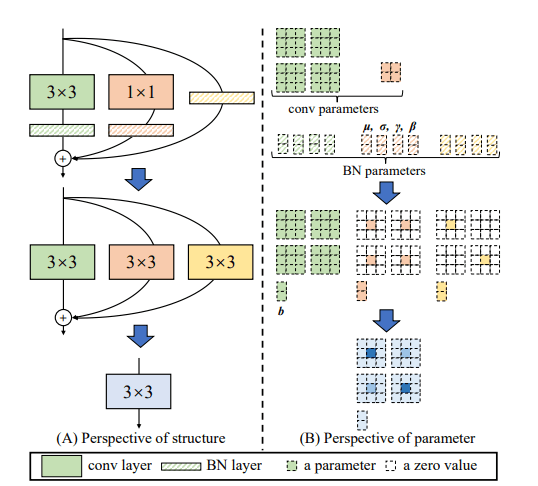
Re-param

请注意，我们在每个分支中使用BN，一般来说，我们使用 $W^{(3)} \in \mathbb{R}^{C_2 \times C_1 \times 3 \times 3}$ 表示输入为 $C_1$ ，输出为 $C_2$ 的 $3 \times 3$ 卷积层。 $W^{(1)} \in \mathbb{R}^{C-2 \times C_1}$ 表示 $1 \times 1$ 卷积层。使用 $\mu^{(3)}$ ， $\sigma^{(3)}$ ， $\gamma^{(3)}$ ， $\beta^{(3)}$ 作为累加平均数、标准差和学习到的缩放因子以及 $3×3$ conv之后的BN层的偏置。 $1 \times 1$ 的为 $\mu^{(1)}$ ， $\sigma^{(1)}$ ， $\gamma^{(1)}$ ， $\beta^{(1)}$ ，Identity链接分支为 $\mu^{(0)}$ ， $\sigma^{(0)}$ ， $\gamma^{(0)}$ ， $\beta^{(0)}$ ， $M^{(1)}$ 作为输入， $M^{(2)}$ 作为输出，当 $C_1 = C_2$ ， $H_1 = H_2$ ， $W_1=W_2$ ，我们有：

M^{(2)} = \text{bn}(M^{(1)} * W^{(3)},\mu^{(3)},\sigma^{(3)},\gamma^{(3)},\beta^{(3)})\\ + \text{bn}(M^{(1)} * W^{(1)},\mu^{(1)},\sigma^{(1)},\gamma^{(1)},\beta^{(1)})\\ + \text{bn}(M^{(1)},\mu^{(0)},\sigma^{(0)},\gamma^{(0)},\beta^{(0)})

否则，我们干脆不使用Identity分支，因此上式中只有前两个项。这里 $\text{bn}$ 是推理时间的BN函数，形式上，$\forall1 \leq i \leq C_2 $。

\text{bn}(M,\mu,\sigma,\gamma,\beta)_{:,i,:,:} = (M_{:,i,:,:} - \mu_i)\frac{\gamma_i}{\sigma_i} + \beta_i

我们首先将每个BN及其前面的conv层转换为带有偏置向量的conv。让 $\{W^\prime , b^\prime\}$ 是由 $\{ W,\mu,\sigma,\gamma,\beta \}$ 转换的核和偏置，我们有

W^\prime_{i,:,:,:} = \frac{\gamma_i}{\sigma_i}W_{i,:,:,:},b^\prime_i=-\frac{\mu_i\gamma_i}{\sigma_i} + \beta_i

那么很容易验证，$\forall1 \leq i \leq C_2 $

\text{bn}(W * M,\mu,\sigma,\gamma,\beta) _{:,i,:,:} = (M * W^\prime)_{:,i,:,:} + b^\prime_i

这种转换也适用于Identity分支，因为一个身份可以被看作是一个以Identity矩阵为核的 $1 \times 1$ conv。经过这样的转换，我们将有一个 $3×3$ 内核，两个 $1×1$ 内核，以及三个偏置向量。然后，我们通过将三个偏置向量相加得到最终的偏置，通过将 $1×1$ 核加到 $3×3$ 核的中心点上得到最终的 $3×3$ 核，如图上所示。请注意，这种变换的等效性要求 $3×3$ 和 $1×1$ 层具有相同的步长，而且后者的padding应比前者少一个像素。例如，对于一个 $3×3$ 层的输入填充一个像素， $1×1$ 层应该为 $\text{padding} = 0$ 。

架构规格

RepVGG不像VGG那样使用最大池化，因为我们希望主体只有一种类型的运算符。我们将 $3×3$ 层排列成 $5$ 个阶段，一个阶段的第一层以 $\text{stride}=2$ 进行降采样。

对于分类任务，使用全局平均集合，然后跟随全连接层作为分类头。对于其他任务，特定任务的头可以用在任何一层产生的特征上。

我们按照三个简单的准则决定每个阶段的层数。

第一阶段以高分辨率操作，这很耗时，所以我们只用一层来降低延迟。
最后一个阶段应具有更多的通道，所以我们只用一层来节省参数。
我们将最多的层放入最后的第二个阶段（在ImageNet上有 $14×14$ 的输出分辨率），遵循ResNet及其最近的变体]（例如，ResNet-101在其 $14×14$ 分辨率阶段使用69层）。