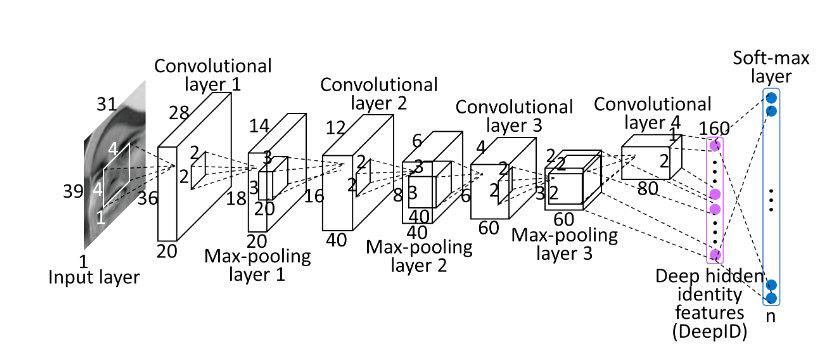
Paper Reading: SiamFC
介绍
新的完全卷积的基于孪生结构的架构,名为Siamse,用于追踪任意物体,且不需要在线学习。
在初始离线阶段训练深度转换网络来解决更一般的相似性学习问题,然后在跟踪过程中在线简单地评估该函数。该方法在现代跟踪基准测试中以远远超过帧速率要求的速度实现了非常有竞争力的性能。
我们训练Siamese网络在较大的搜索图像中定位示例图像。需要跟踪的对象仅由第一帧中的矩形区域识别。
用于跟踪的深度相似学习
追踪任意物体的学习可以用相似性学习来解决。学习一个深度卷积神经网络 ,该函数将示例图像 与相同大小的候选图像 进行比较,返回相似度评分。为了找到物体在新图像中的位置,我们可以详尽地测试所有可能的位置,并选择与该物体过去的外观相似度最高的候选。在实验中,我们将简单地使用物体的初始外观(第一帧中的)作为典范。
深度卷积网络的相似性学习通常使用孪生结构来解决。孪生网络对两个输入应用相同的变换 ,然后根据 用另一个函数 组合它们的表示。本文中 是一个简单的距离或相似度量, 是一个嵌入(CNN)。
全卷积孪生结构
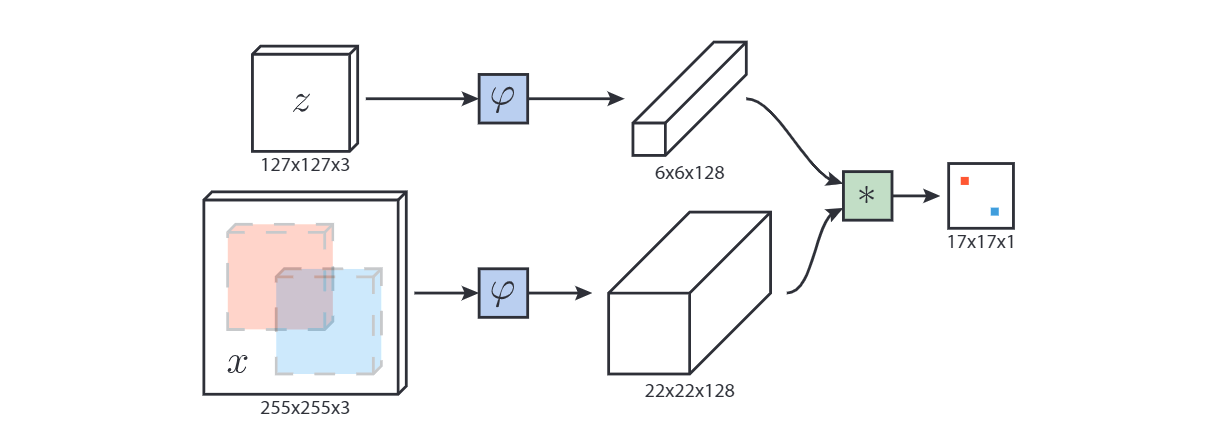
我们使用卷积嵌入函数φ,并使用互相关层将得到的特征图结合起来:
其中 表示在每个位置上取值 的信号。输出是一个定义在有限网格 上具有空间信息的分数图。在追踪过程中,我们使用以目标的先前位置为中心的矩形图片作为搜索图像(以上一帧预测的边缘框的中心为裁剪中心,裁剪出255x255大小的图片,如下图)。
使用大型搜索图像进行学习
我们采用了一种鉴别性的方法,对正反两方面的网络进行训练,并采用逻辑损失法:
其中,是网络输出的单个exemplar-candidate对的实值分数, 是ground truth标签。在训练过程中,我们利用我们的网络的完全卷积性质,使用由一个示范图像和一个更大的搜索图像组成的配对。这将产生一个分数图,有效地产生了每一对的许多例子。我们将一个分数图的损失定义为单个损失的平均值
要求对分数图中的每个位置 有一个真实标签 。卷积网络的参数 是通过SGD来学习得到的:

在不破坏图像长宽比的情况下,每个图像内物体的比例被归一化。即当模板和搜索图像不够裁剪时,要对不足的像素进行RGB通道的均值填充,如上图。
分数图中的元素如果在中心的半径范围内,则被认为属于正例(考虑到网络的步长):