Paper Reading: FaceNet
现有的方法无法大规模有效的实施人脸验证和识别。因此,我们提出了一种称为FaceNet的系统,该系统直接从人脸图像学习映射到紧凑( 维)的欧氏空间,其距离直接对应于人脸相似性的度量。一旦产生了这个空间,就可以很容易地基于FaceNet的嵌入向量使用k-NN进行人脸识别,K-means实现聚类。
我们的方法使用一个CNN进行训练,直接优化嵌入本身。而不是使用间接的和低效率的中间瓶颈层。为了训练,我们使用了用一种新颖的在线三联体挖掘方法生成的大致一致的匹配/不匹配的脸部patch的三联体(三个对脸部区域的紧密剪裁,除了缩放和平移之外,没有进行二维或三维对齐的裁剪。两个匹配的面部与一个不匹配的面部)。
我们实现了最先进的人脸识别性能,每张脸只用128字节。
我们还介绍了harmonic嵌入的概念,以及harmonic三联体损失,它描述了不同版本的脸部嵌入(由不同的网络产生),它们彼此兼容,并允许彼此之间进行直接比较。
为了提高聚类的准确性,我们还探索了hard-positive挖掘技术,鼓励对单个人的嵌入进行球形聚类。
关键词:三联体、harmonic嵌入、三联体损失。
Method
我们努力寻求一个嵌入 ,从一个图像 到一个特征空间 ,使得独立于成像条件的同一身份的所有面孔之间的平方距离很小,而来自不同身份的一对面孔图像之间的平方距离则很大。
三元体损失
嵌入由 表示,我们把这个嵌入限制在 维的超球上,。在这里,我们要确保一个特定人的图像 (锚)与同一个人的所有其他图像(正样本)相比,更接近于任何负样本 。
其中 是一个边缘,在正反两方面之间强制执行。是训练集中所有可能的三联体的集合,其基数为 。那么被最小化的损失就是
三元体选择
在选择上尽量违反第一个公式,即给定 我们想要选择一个 使得 (与正样本尽可能差距大),(与负样本尽可能像)。
计算整个训练集的 和 是不可行的。此外,这可能会导致训练效果不佳,因为错误的标签和成像不佳的面孔会在硬正样本和负样本中占主导地位。有两个明显的选择可以避免这个问题:
- 每隔
n步离线生成三联体,使用最近的网络检查点并计算数据子集的 和 。
在这里,我们专注于在线生成,并使用几千个样本的大型迷你批次,只计算迷你批次中的 和 。
为了对锚点-正样本距离进行有意义的表述,需要确保每个小批中都有最少数量的任何一个身份的典范存在。在我们的实验中,我们对训练数据进行了抽样,使每个小批中的每个身份都有大约40张脸被选中。 此外,随机抽样的负样本面孔被添加到每个小批次中。
在实践中,选择最难的负数可能会导致训练初期出现不好的局部最小值,特别是可能导致模型坍塌(即 )。 为了减轻这种情况,选择是有帮助的,即
忽略了损失函数中的
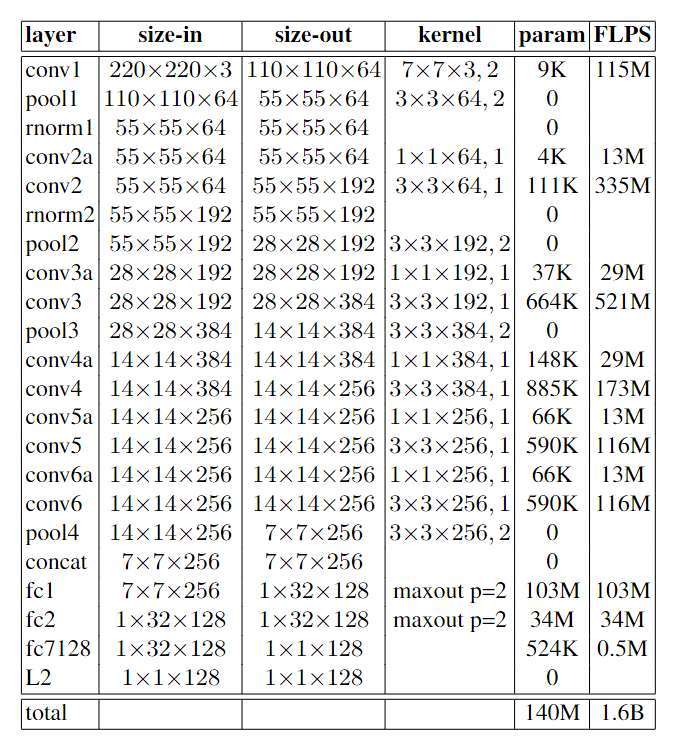
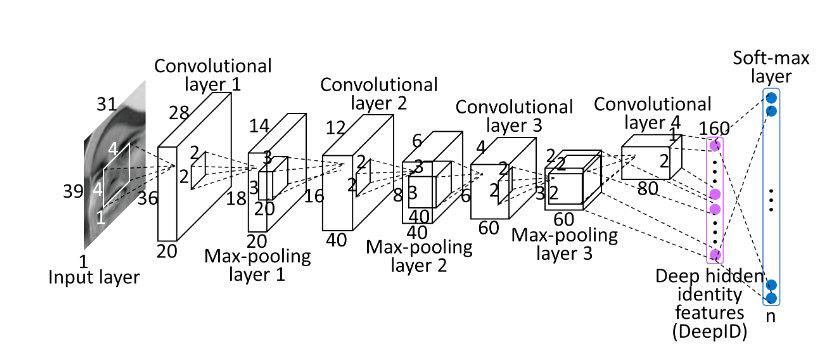
深度卷积神经网络