介绍

新颖、简单而有效的车道检测方案，通过选择车道的位置而非语义分割对每个像素进行预测，从而效率更高。使用全局特征预测，可以有效的解决无视觉线索的难题。
提出结构性损失，明确地利用车道的先验知识，如车道的刚性和平滑度等。

方法

将车道检测改转变为基于全局图像特征的行式选择方法，即使用全局特征在每个预定的行上选择正确的车道位置。

在我们的方法中，车道被表示为一系列预定的行中的水平位置，即行锚。在每个行锚上，位置被分为许多单元。以这种方式，车道的检测可以被描述为在预定的行锚上选择某些单元。

设最大车道数为 $C$ ，行锚数为 $h$ ，网格单元的数量为 $w$ 。假设 $X$ 是全局图像特征， $f^{ij}$ 是用于选择第 $i$ 条车道线和第 $j$ 行锚上的车道位置的分类器。那么车道的预测可以写成：

P_{i,j,:}=f^{ij},\text{s.t.} i \in [1,C],j\in [1,h]

其中 $P_{i,j}$ 是 $(w+1)$ 维向量（我们用一个额外的维度来表示没有车道的情况），表示在第 $i$ 车道线，第 $j$ 行锚选择第 $w+1$ 个网格单元的的概率。假设 $T_{i,j,:}$ 是正确位置的one-hot标签。那么，我们方法需要优化的是：

L_{cls}=\sum^C_{i=1}\sum^h_{j=1}L_{CE}(P_{i,j,:},T_{i,j,:})

其中， $L_{CE}$ 是交叉熵损失函数。

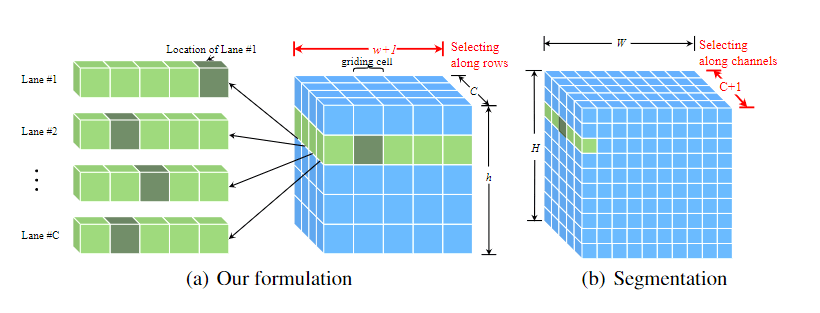
上图为本文方法与分割方法的区别

除了分类损失外，我们还提出了两个损失函数，用于建模车道点的位置关系，使其能够学习结构信息。

第一个是基于车道是连续的这一事实，也就是说，相邻行锚中的车道点应相互靠近。连续属性是通过约束分类向量在相邻行锚上的分布来实现的。这样一来，相似性损失函数可以是：

L_{sim}=\sum^C_{i=1}\sum^{h-1}||P_{i,j,:}-P_{i,j+1,:}||_1

另一个结构性损失函数关注的是车道的形状。一般来说，大多数车道是直的。即使是曲线车道，由于透视效应，它的大部分仍然是直线。我们使用二阶差分方程来约束车道的形状，对于笔直的情况，这个方程是零。对于任何车道索引 $i$ 和行锚索引 $j$ ，位置 $Loc_{i,j}$ 可以表示为：

Loc_{i,j}=\argmax_k P_{i,j,k},\text{s.t.}k\in [1,w]

其中 $k$ 是表示位置索引的整数，需要注意的是，我们不计算背景网格单元，而且位置索引k的范围只有 $1$ 到 $w$ ，而不是 $w+1$ 。

然而，argmax是不可微的，不能用于进一步的约束。此外，在分类表述中，类没有明显的顺序，很难在不同的行锚之间建立关系。为了解决这个问题，我们建议使用预测的期望值作为位置的近似值。我们使用softmax函数来获得不同位置的概率。

Prob_{i,j,:}=softmax(P_{i,j,1:w})

代表每个位置的概率。

位置的期望值可以写成：

Loc_{i,j}=\sum_{k-1}^w k\cdot Prob_{i,j,k}

是第 $i$ 条车道、第 $j$ 个行锚和第 $k$ 个位置的概率。

二阶差分约束可写为：

L_{shp}=\sum^C_{i=1}\sum^{h-2}_{j=1}||(Loc_{i,j}-Loc_{i,j+1})-(Loc_{i,j+1}-Loc_{i,j+2})||_1

我们使用二阶差分而不是一阶差分的原因是，一阶差分在大多数情况下不是零。所以网络需要额外的参数来学习车道位置的一阶差值的分布。此外，二阶差分的约束相对比一阶差分的约束要弱，因此当车道不直时，影响较小。

整体的损失函数为：

L_{str}=L_{sim}+\lambda L_{shp}

在第上文中，损失函数设计主要集中在车道的关系上。在这一节中，我们提出了一种辅助特征聚合方法，该方法在全局背景和局部特征上执行。我们提出了一个利用多尺度特征的辅助分割任务来模拟局部特征。我们使用交叉熵作为我们的辅助分割损失。这样一来，我们方法的总体损失可以写成。

L_{total}=L_{cls}+\alpha L_{str}+\beta L_{seg}

其中 $L_{seg}$ 是分割损失， $\alpha$ 和 $\beta$ 是损失系数。整体结构如下图所示

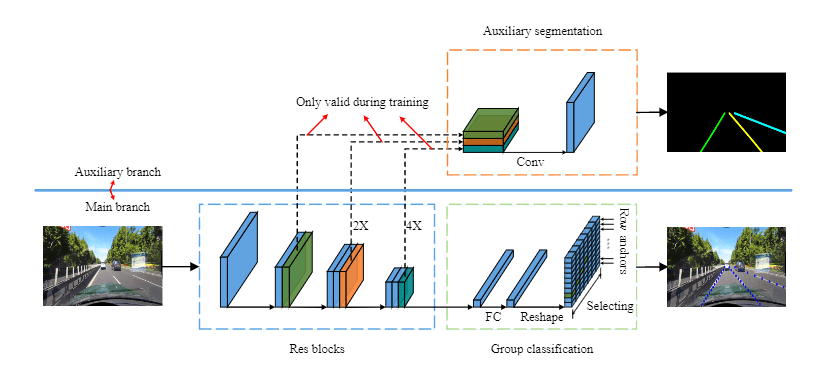
我们的方法只在训练阶段使用了辅助分割任务，而在测试阶段会将其删除。