介绍

本文研究了网络设计的另一个方面——特征在通道之间的关系

我们提出了一个新的架构单元，称之为Squeeze-and-Excitation(SE) 块，其目的是通过明确地建模特征图通道之间的依赖关系来提高网络产生的表征的质量，利用全局信息，有选择地强调和压制特征。

SE块的结构如下图，

FtrF_{tr} 是任意给定的变换（例如一个卷积），他将输入 XX 映射到特征图 UU，其中 U∈RH×W×CU \in \mathbb{R}^{H \times W \times C}

特征图 UU 首先经过一个名为 Squeeze 的操作，它通过在空间维度（ H×WH \times W ）上聚合特征图来生成通道特征响应的全局分布的 Embedding，使网络的全局接收场的信息被其所有层使用。

聚合特征图后（经过 Squeeze 后），跟随一个名为 excitation 的操作，它采用一种简单的自我门控机制，将嵌入作为输入，产生一组对于每个通道的权重

这些权重最终被应用于特征图 UU ，生成SE块的输出，随货直接输入网络的后续层。

虽然 SE 块是通用的，但在整个网络中，它在不同深度作用也不同。

在前几层，它以一种与类别无关的方式突出了信息特征,加强共享的低层次表征

在后面的层中，SE块变得越来越对于不同类别专门化，并以高度特定类的方式对不同的输入作出反应。

因此，由 SE 块进行的特征重新校准的增益可以通过网络累积。

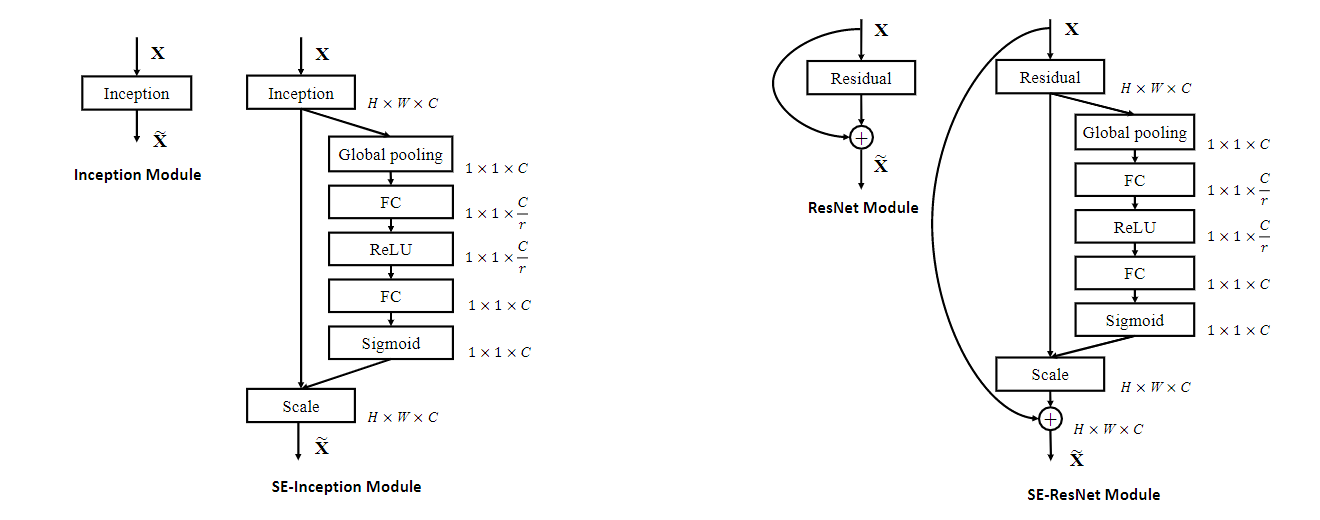
SE 块的结构很简单，可以直接在现有最先进的网络架构中使用，方法是用 SE 块替换组件，即可显著提升网络性能，且只增加了少量计算成本。

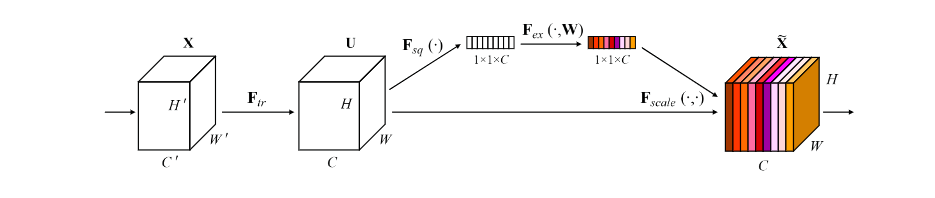
Squeeze-and-excitation 块

SE 块是一个建立在一个变换 FtrF_{tr} 上的计算单元。

FtrF_{tr} 将输入 X∈RH′×W′×C′X \in \mathbb{R}^{H^\prime \times W^\prime \times C^\prime} 映射到特征图 U∈RH×W×CU \in \mathbb{R}^{H \times W \times C}。

我们取 FtrF_{tr} 为一个卷积操作，用 V=[v1,v2,...,vC]V=[v_1,v_2,...,v_C] 来表示所学到的卷积核的集合。

我们将输出写作 U=[u1,u2,...,u3]U = [u_1,u_2,...,u_3]，其中

uc=vc∗X=∑s=1C′vcs∗xsu_c = v_c * X = \sum^{C^\prime}_{s=1}v^s_c * x^s

这里 ∗* 代表卷积，vc=[vc1,vc2,...,vcC′]v_c = [v^1_c,v^2_c,...,v^{C^\prime}_c]，uc∈RH×Wu_c \in \mathbb{R}^{H \times W}。vcsv^s_c是一个 2D 空间下的核，代表 vcv_c 中的单独一个通道，作用于 XX 的相应通道上。为了简化符号省略了偏置项。

由于输出是通过所有通道的求和产生的，通道依赖性被隐含地嵌入vcv_c,，但与滤波器捕捉到的局部空间相关性杂糅。

卷积所建模的通道关系本质上是隐式的且局部的，所以我们希望卷积特征的学习能够通过明确地建模通道的相互依赖性而得到加强，这样网络就能够提高其对信息特征的敏感性，这些特征可以被后续的转化所利用。

因此我们想让它获得全局信息，并重新校准特征图。

Squeeze：全局信息 Embedding

每一个学习到的滤波器都在一个局部的接受领域内运行，因此，变换输出的每个单元U都无法利用这个区域以外的上下文信息。

为了缓解这个问题，我们将全局空间信息压缩到一个通道描述符中。

我们通过使用全局平均池化来产生逐通道的统计数据来实现的。

统计数据 z∈RCz \in \mathbb{R}^C ，他通过收缩U的空间维度 H×WH×W 产生。

zz 的第 cc 个元素的计算方法如下：

zc=Fsq(uc)=1H×W∑i=1H∑j=1Wuc(i,j)z_c = F_{sq}(u_c) = \frac{1}{H \times W}\sum ^H_{i=1}\sum^W_{j=1}u_c(i,j)

Excitation：自适应重新校准

为了利用在挤压操作中汇总的信息，我们紧接着进行了第二个操作，使用一个简单的门控机制，采用sigmoid激活函数：

s=Fex(z,W)=σ(g(z,W))=σ(W2δ(W1z))s = F_{ex}(z,W)=\sigma(g(z,W))=\sigma(W_2\delta(W_1z))

其中 δ\delta 是 ReLU，W1∈RCr×CW_1 \in \mathbb{R}^{\frac{C}{r} \times C}，W2∈RC×CrW_2 \in \mathbb{R}^{C \times \frac{C}{r}}

为了限制模型的复杂性和帮助推广，我们通过在非线性周围的两个 FC层 形成一个瓶颈来对门控机制进行参数化。即具有降低率 rr的降维层（本文中r=16r = 16）。 一个ReLU，然后是一个增维层，还原到变换 FtrF_{tr} 输出的 UU 的通道维度。

块的最终输出是通过用ss重新缩放UU得到的：

x~c=Fscale(uc,sc)=scuc\widetilde{x}_c = F_{scale}(u_c,s_c)=s_cu_c

其中 X~=[x~1,x~2,...,x~C]\widetilde{X} = [\widetilde{x}_1,\widetilde{x}_2,...,\widetilde{x}_C]，Fscale(uc,sc)F_{scale}(u_c,s_c)是scs_c和特征图 uc∈RH×Wu_c\in \mathbb{R}^{H\times W} 按通道相乘得到.

实例化